• Impressum & Datenschutz

Keywords: Soft exponential growth functions; inverse functions

Abstract

It is shown, that Planck's Law of radiation can be seen as the Law of Rayleigh-Jeans, superposed by a descending soft exponential function. A class of such functions is given.

Introduction

In the last decade of the 19^th century three famous physicists (all nobel prize winners) published formulas of the intensity of radiation in dependence on (absolute) temperature T and frequency ν

I. Rayleigh's and Jeans' formula was

(R) 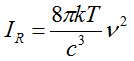(1a)

(with the nomenclature after Planck's publication: k is Boltzmann's constant, c is speed of light). Formula (R) gives good correspondence of theory and experience (data) for small values of ν, but wide divergence for great values of ν

II. Wien gave the formula

(W)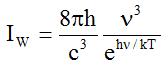 (2a)

with Planck's constant constant h. This hypothesis gives good correspondence with the data for high frequencies ν, but a bad one for small frequencies.

III. In 1900 Planck finally gave the formula

(P)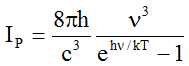(3a)

which gives good correspondence with the data for all values of ν.

Standardization

By introducing x=hν/kT, we get from (1a)

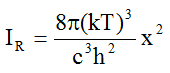
and with 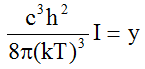y_R = x² (1b)

Correspondingly 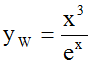(2b)

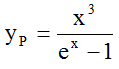and (3b)

i.e. for fixed T three relative simple functions in the standardized variables x and y (see fig. 1).

Fig. 1: Curves of Rayleigh, Wien, Planck and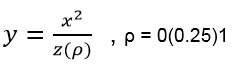

Formula (1b) is a simple parabolic growing function of x. If you imagine data along the "right", i.e. along Planck's curve in figure 1, you see, that for smaller values of x the ascending trend of the data is well approximated by formula (1b), while for greater values of x we have huge overestimation: The descending trend of the data is in no way realized. This would cause the so-called "ultraviolet-catastrophe".

So a descending trend-term must be superposed to formula (1b) of Rayleigh and Jeans. The best-known term is the descending exponential function e^-x. But the result y₁=x²e^-x yields by far too small values of y for all values of x, compared with our imagined data (see figure 1). So it seems near at hand, to superpose a further ascending term to y₁. The simplest one is y₂=x. Probably this was Wien's reasoning, too. The final result is formula (2b). This hypothesis approximates the "data-points" very well for great values of x, but underestimates the data for smaller values of x.

Consequences from the results of Rayleigh-Jeans and Wien

We write formulas (1b) and (2b) in the form

y_R = x²y_R0 with y_R0 = 1(1c)

and y_W = x²y_W0 with y_W0 = xe^-x(2c)

We have two boundary conditions for the "right" formula y = x²y₀, namely

y₀(x) → 1 for x → 0 and y₀(x) → xe^-x for x → ∞(4a/b)

(see figure 2).

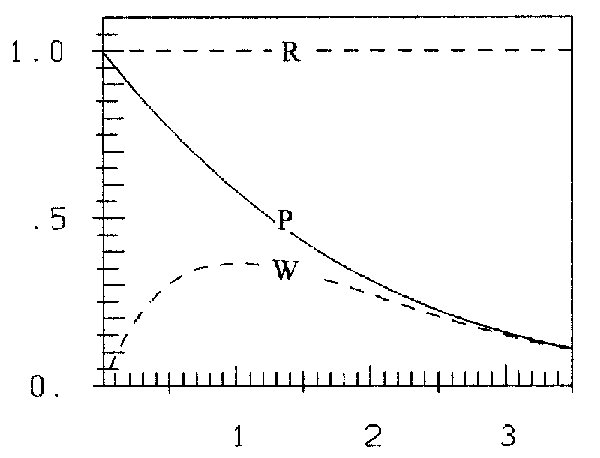
Fig. 2: Multipliers y_•0 for hypothesis

The most simple and reasonable hypothesis for y₀ is

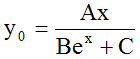, or with b=B/A, c=C/A: 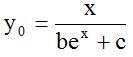(5)

So we have two conditions (4) for the two parameters a and b.
Because of condition (4a) c cannot be zero; because of (4b) we have b=1. Then because of (4a) there must be c=-1. For this write e^x as Taylor series. So finally we have

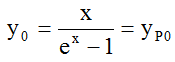(6)

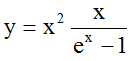and (7)

i.e. Planck's Law.

Supplement

I will call (6) the inverse of a soft exponential growth function, and accordingly

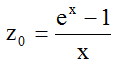(8)

a soft exponential growth function. The name "soft" comes from the fact, that the growth of z₀ is smaller (softer) than that of e^x (see figure 3a). Accordingly the decline of y₀ is smaller than that of e^-x (figure 3b).

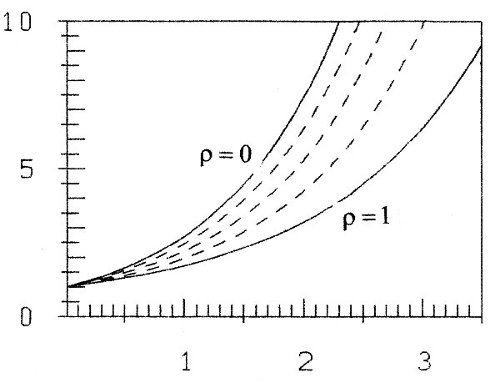
Fig. 3a: Soft exponential growth functions z(ρ)
ρ = 0, 0.25, 0.5, 0.75, 1

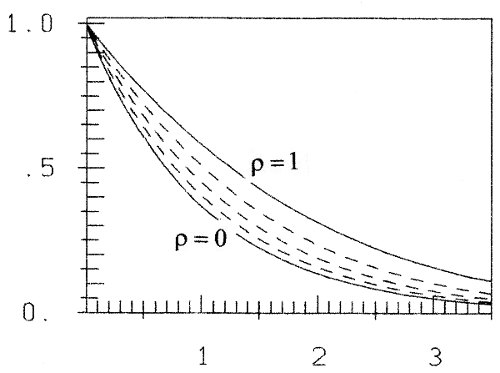
Fig. 3b invers to figure 3a: 1/z(ρ)

Then with e^x and z₀ we have a class of soft exponential growth functions:

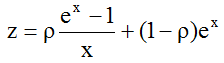; 0 ≤ ρ ≤ 1 (9)

and with 1/z a class of inverses (see figures 3 with ρ = 0, 0.25, 0.5, 0.75, 1).

In figure 1 the curve 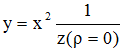is plotted (Wien's first step y₁ - as I assume). Further steps for ρ = 0.25, 0.5, 0.75, 1 (dotted curves) lead to Planck's curve.

References