Planck's Law: A Mathematical Deduction from the Law of Rayleigh-Jeans and the Law of Wien
H. Schneeberger
Institute of Statistics, University of Erlangen-Nürnberg, Germany
2015, 9th February
Keywords: Soft exponential growth functions; inverse functions
Abstract
It is shown, that Planck's Law of radiation can be seen as the Law of Rayleigh-Jeans, superposed by a descending soft exponential function. A class of such functions is given.
Introduction
In the last decade of the 19th century three famous physicists (all nobel prize winners) published formulas of the intensity of radiation in dependence on (absolute) temperature T and frequency ν
I. Rayleigh's and Jeans' formula was
(R) 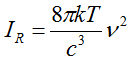 (1a)
(1a)
(with the nomenclature after Planck's publication: k is Boltzmann's constant, c is speed of light). Formula (R) gives good correspondence of theory and experience (data) for small values of ν, but wide divergence for great values of ν
II. Wien gave the formula
(W)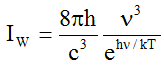 (2a)
(2a)
with Planck's constant constant h. This hypothesis gives good correspondence with the data for high frequencies ν, but a bad one for small frequencies.
III. In 1900 Planck finally gave the formula
(P)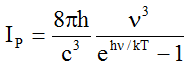 (3a)
(3a)
which gives good correspondence with the data for all values of ν.
Standardization
By introducing x=hν/kT, we get from (1a)
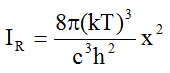
and with 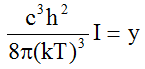 yR = x2 (1b)
yR = x2 (1b)
Correspondingly 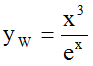 (2b)
(2b)
and 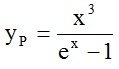 (3b)
(3b)
i.e. for fixed T three relative simple functions in the standardized variables x and y (see fig. 1).

Fig. 1: Curves of Rayleigh, Wien, Planck and 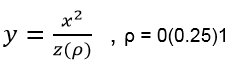
Formula (1b) is a simple parabolic growing function of x. If you imagine data along the "right", i.e. along Planck's curve in figure 1, you see, that for smaller values of x the ascending trend of the data is well approximated by formula (1b), while for greater values of x we have huge overestimation: The descending trend of the data is in no way realized. This would cause the so-called "ultraviolet-catastrophe".
So a descending trend-term must be superposed to formula (1b) of Rayleigh and Jeans. The best-known term is the descending exponential function e-x. But the result y1=x2e-x yields by far too small values of y for all values of x, compared with our imagined data (see figure 1). So it seems near at hand, to superpose a further ascending term to y1. The simplest one is y2=x. Probably this was Wien's reasoning, too. The final result is formula (2b). This hypothesis approximates the "data-points" very well for great values of x, but underestimates the data for smaller values of x.
Consequences from the results of Rayleigh-Jeans and Wien
We write formulas (1b) and (2b) in the form
yR = x2yR0 with yR0 = 1(1c)
and yW = x2yW0 with yW0 = xe-x(2c)
We have two boundary conditions for the "right" formula y = x2y0, namely
y0(x) → 1 for x → 0 and y0(x) → xe-x for x → ∞(4a/b)
(see figure 2).
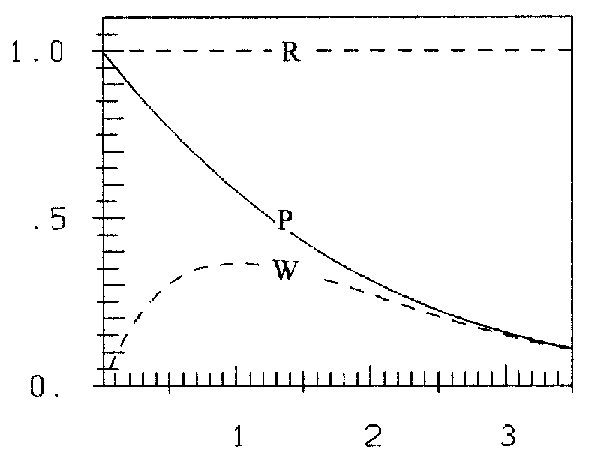
Fig. 2: Multipliers y•0 for hypothesis ![]()
The most simple and reasonable hypothesis for y0 is
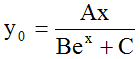 , or with b=B/A, c=C/A:
, or with b=B/A, c=C/A: 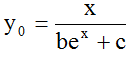 (5)
(5)
So we have two conditions (4) for the two parameters a and b.
Because of condition (4a) c cannot be zero; because of (4b) we have b=1. Then because of (4a) there must be c=-1. For this write ex as Taylor series. So finally we have
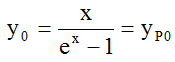 (6)
(6)
and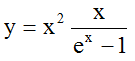 (7)
(7)
i.e. Planck's Law.
Supplement
I will call (6) the inverse of a soft exponential growth function, and accordingly
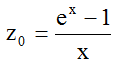 (8)
(8)
a soft exponential growth function. The name "soft" comes from the fact, that the growth of z0 is smaller (softer) than that of ex (see figure 3a). Accordingly the decline of y0 is smaller than that of e-x (figure 3b).
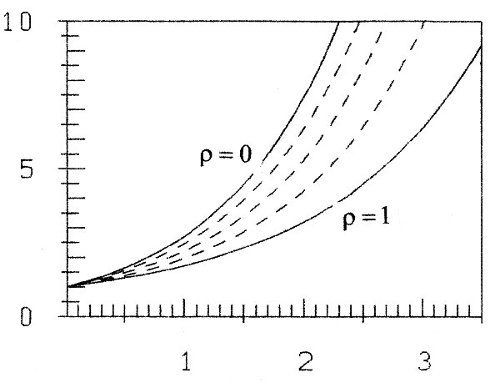
Fig. 3a: Soft exponential growth functions z(ρ)
ρ = 0, 0.25, 0.5, 0.75, 1
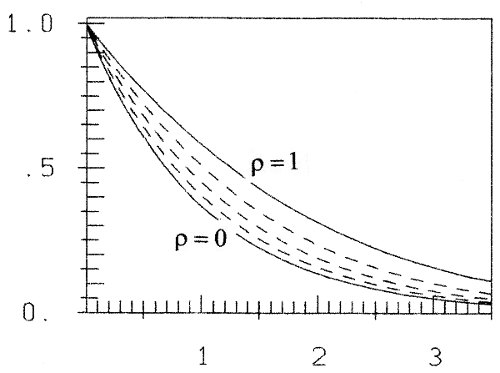
Fig. 3b invers to figure 3a: 1/z(ρ)
Then with ex and z0 we have a class of soft exponential growth functions:
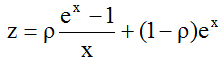 ; 0 ≤ ρ ≤ 1
(9)
; 0 ≤ ρ ≤ 1
(9)
and with 1/z a class of inverses (see figures 3 with ρ = 0, 0.25, 0.5, 0.75, 1).
In figure 1 the curve 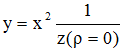 is plotted (Wien's first step y1 - as I assume). Further steps for ρ = 0.25, 0.5, 0.75, 1 (dotted curves) lead to Planck's curve.
is plotted (Wien's first step y1 - as I assume). Further steps for ρ = 0.25, 0.5, 0.75, 1 (dotted curves) lead to Planck's curve.
References
Planck, M.: Über eine Verbesserung der Wienschen Spektralgleichung; Verhandlungen der dt. phys. Ges. Berlin, Jhg.2, Nr.13 (1900), pp. 202-204
Planck, M.: Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum; Verhandlungen der dt. phys. Ges. Berlin, Jhg.2, Nr. 17 (1900), pp.237-252
Download this paper as PDF
Download this Paper in PDF format:
Planck's Law: A Mathematical Deduction from the Law of Rayleigh-Jeans and the Law of Wien [PDF, 403 kB]